浅谈DDPM重要的推导公式

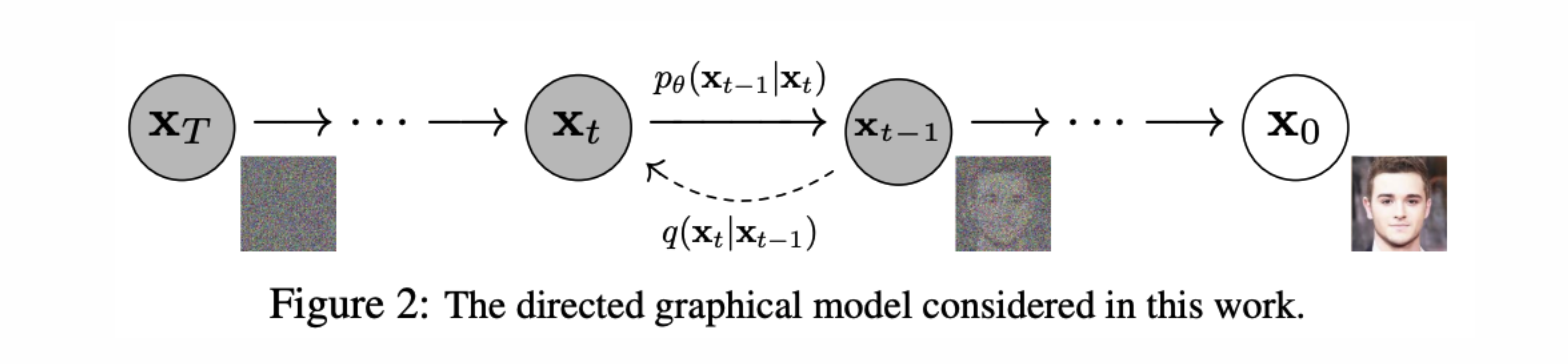
DDPM，Denoising Diffusion Probabilistic Models，以其生成细节丰富，指标优秀而闻名。广为人知的是其正向加噪的马尔可夫链和逆向过程，但是概率公式推导却少有人真正掌握得得心应手。在此浅谈，更多是记录，以做“烂笔头”的用。

Forward Process

基础假设

众所周知，DDPM前向过程基于一个巧妙的假设：

从概率学的角度理解，这符合了马尔可夫链(Markov Chain)的性质

马尔可夫链

下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。

因此有链式法则

初次看这个公式是不显然的，隐含了很多很多假设

我们把它拆开，右边就是

可以变形成

这样分子的最右边两项可以合并

根据马尔可夫链的性质，每一个状态的概率分布仅由前一状态决定，与其他时间无关，因此有

因此上分式有

因此分子可以合并为

这样推导是抽象的。

具体推导

具体到扩散过程的假设：

其中，和独立同分布，因此可以合并

我们发现形式与开头的假设完全相同；可以继续推下去，直到，形式都是相同的，因此

令，因此从“前向过程可以看作似然函数”的角度可以表示为

总结

回看开头提到的“巧妙”的假设，巧妙在其不仅遵循了马尔可夫链的性质——概率分布满足链式法则，同时推导过程也满足链式法则。概率分布满足链式法则奠定了扩散理论有效的理论基础；推导过程满足链式法则使得理论的实施成为可能（能够一步完成T步变换），也提高了可解释性（尝试使用”线性“来拟合）。本质上，这两者是统一的，但这一统一是基于基本假设的。这便是这个假设的巧妙之处，也是扩散模型的精髓。

Reverse Process

Reverse Process即正向过程的逆，从去噪得到的过程。

对上面的转换公式进行变形就可以得到

这时候不妨设想，是否直接按照链式法则得到的降噪公式，学习多个独立同分布变量合成的噪声，就能实现生成？

从感性的角度想，因为真实图像的分布是极其复杂的，使用一步去拟合是不现实的（DDPM论文中也提到，这么做生成的图像会很模糊）。

但是，从理性的角度分析，不免感到困惑：既然这个马尔可夫链具有链式法则，那和在数学上就具有了简单的加噪等式关系，和也就具有了简单的去噪等式关系。按上面的说法，这个等式关系是不准确的，因为其中的高维的、复杂的变换是难以表示的。所以导致数学上和实际有巨大出入的原因到底在哪？

这一问题我们放在最后讨论。

马尔可夫链对或错？

对上述问题的看法

在这里对刚才留下的问题发表一些看法：

回到Forward Process的基础假设上，对于这个假设，我们从形式上认为它符合了马尔可夫链的性质，因此按照马尔可夫链的性质我们认为当前状态和除上一状态以外的其他状态都独立。这一观点在公式推导过程中出现了

根据马尔可夫链的性质，每一个状态的概率分布仅由前一状态决定，与其他时间无关，因此有

这里就引出了一个”条件独立性“的问题：

在数学上，我们可以认为当前状态只与上一状态有关。但在实际的生成图像的情景中，各个步骤显然是不完全独立的。因此上述问题中的关键就在于此：因为马尔可夫链性质的数学假设，导致了和之间得到的简单的加噪等式与实际情况出现了出入（这点映证了感性的理解），因此我们无法直接使用简单的一步去噪得到。

对问题本质的反思

这时候反思，这样的问题是当前情境独有的吗？显然不是。

马尔可夫链本身不就具有这种问题吗，“每一个状态只和前一个状态有关”，这显然会导致，从现实角度说，当前状态必定与前前状态是不独立的。所以这能说马尔可夫链理论是错的吗？怎么去理解它呢？这是一个非常有趣且深刻的问题。

马尔可夫链的核心假设确实是每个状态只依赖于前一个状态（即马尔可夫性质），但这并不意味着马尔可夫链的理论是“错”的。相反，这种假设提供了一种简化的模型，能够有效地捕捉很多实际问题中的动态系统行为。这种性质允许我们简化复杂系统的分析，把一个复杂的、高维的映射过程近似地拆解成多个简单的、低纬的映射，以更好地拟合目标分布。

总而言之，马尔可夫链只是一种对现实世界的近似建模方式，在建模时，选择是否使用马尔可夫假设通常涉及到权衡，简单的模型更容易理解、计算和实现，但可能会丧失一些准确性；复杂的非马尔可夫模型可能会捕捉到更多的信息，但其计算和实现上会更加复杂。在DDPM中，使用马尔可夫链很好地拆解了从像素空间到潜空间这个映射关系，把它以”逐步加噪“的形式呈现。

一些启发

一种对马尔可夫假设的扩展是多阶马尔可夫链，其中当前状态依赖于多个之前的状态。例如，二阶马尔可夫链将前两个状态考虑在内。虽然使得模型更加复杂，但可以更准确地描述某些系统。这种想法是否可以解决一些扩散模型因马尔可夫链的信息丢失而低效的问题？

Chandery's Blog